First order logic (首階邏輯 / ㄧ階邏輯)

除了希臘字母

寫Algorithm或computer science方面的paper

常用到正規(正式/形式)演繹系統(formal deductive system)

這套演繹系統叫做"First order logic" (FOL)

有人翻譯成"首階邏輯"

Wikipedia裡則是翻譯成"ㄧ階邏輯"

為什麼需要FOL呢?

FOL使用正式或正規已定義好的符號跟用法來敘述邏輯關係

以解決自然語言, 如英文, 無法直接程式化的問題

上面兩個連結就是Wikipedia裡的英文跟中文兩個版本的連結

(中文版翻得不是很順, 建議看英文版)

不過貼完就天黑了

有需要的人自己連進去看

這邊僅收錄Logical symbols及其變化:

"Logical symbols

Besides logical connectives such as , , 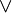, 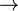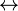and , the logical symbols include quantifiers, and variables.

1. An infinite set of variables, often denoted by lowercase letters at the end of the alphabet x, y, z,... .


2. Symbols denoting logical operators (or connectives):
   
   
   
   • The unary operator (logical not).
   
   
   • Binary operators (logical and) and 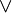(logical or).
   
   
   • Binary operators 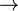(logical conditional) and 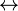(logical biconditional).
   
   
   
   


3. Symbols denoting quantifiers: 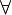(universal quantification, typically read as "for all") and 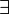(existential quantification, typically read as "there exists").


4. Left and right parenthesis: ( and ). There are many different conventions about where to put parentheses; for example, one might write 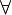x or (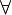x). Sometimes one uses colons or full stops instead of parentheses to make formulas unambiguous. One interesting but rather unusual convention is "Polish notation", where one omits all parentheses, and writes 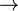, , and so on in front of their arguments rather than between them. Polish notation is compact and elegant, but rare because it is hard for humans to read it.


5. An identity symbol (or equality symbol) =. Syntactically it behaves like a binary predicate.

Variations

First-order logic as described here is often called first-order logic with identity, because of the presence of an identity symbol = with special semantics. In first-order logic without identity this symbol is omitted.

There are numerous minor variations that may define additional logical symbols:

• Sometimes the truth constants T for "true" and F for "false" are included. Without any such logical operators of valence 0 it is not possible to express these two constants otherwise without using quantifiers.


• Sometimes the Sheffer stroke (P | Q, aka NAND) is included as a logical symbol.


• The exclusive-or operator "xor" is another logical connective that can occur as a logical symbol.


• Sometimes it is useful to say that "P(x) holds for exactly one x", which can be expressed as x P(x). This notation, called uniqueness quantification, may be taken to abbreviate a formula such as 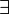x (P(x) 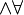y (P(y) 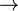(x = y))).

Not all logical symbols as defined above need occur. For example:

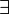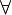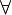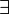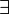• Since ( x)φ can be expressed as (( x)( φ)), and ( x)φ can be expressed as (( x)( φ)), one of the two quantifiers and 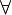can be dropped.


• Since φ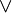ψ can be expressed as (( φ) ( ψ)), and φψ can be expressed as (( φ)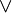 ( ψ)), eithe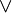r or can be dropped. In other words, it is sufficient to have or as the only logical connectives among the logical symbols.


• Similarly, it is sufficient to have or just the Sheffer stroke as the only logical connectives.

There are also some frequently used variants of notation:

• Some books and papers use the notation φ 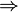ψ for φ 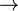ψ. This is especially common in proof theory where 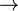is easily confused with the sequent arrow.


• ~φ is sometimes used for φ, φ & ψ for φ ψ.


• There is a wealth of alternative notations for quantifiers; e.g., 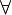x φ may be written as (x)φ. This latter notation is common in texts on recursion theory."

以上"Logical symbols及其變化"轉貼剪輯自(版權): http://en.wikipedia.org/wiki/First-order_logic (retrieved 11/16)